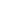最大后验（Maximum a Posteriori，MAP）概率估计详解

最大后验（Maximum A Posteriori，MAP）概率估计

注：阅读本文需要贝叶斯定理与最大似然估计的部分基础

  最大后验（Maximum A Posteriori，MAP）估计可以利用经验数据获得对未观测量的点态估计。它与Fisher的最（极）大似然估计（Maximum Likelihood，ML）方法相近，不同的是它扩充了优化的目标函数，其中融合了预估计量的先验分布信息，所以最大后验估计可以看作是正则化（regularized）的最大似然估计。

  想要了解最大后验（MAP）概率估计，需要学会贝叶斯定理以及极大似然估计（Maximum Likelihood Estimate，MLE）。

1.贝叶斯定理
  贝叶斯定理由英国数学家贝叶斯 ( Thomas Bayes 1702-1761 ) 发展，用来描述两个条件概率之间的关系。
  这里篇博客主要说的并不是贝叶斯定理，因此，只在这里提及需要用到的有关于贝叶斯的部分知识。
  假设，现在有两个一定概率发生的事件A和B，且它们之间存在一定的关系。

   -   P（A）表示事件A发生的概率。
   -   P（B）表示事件A发生的概率。
   -   P（A | B）表示事件B已经发生的情况下，事件A发生的概率。
   -   P（B | A）表示事件A已经发生的情况下，事件B发生的概率。
  
  理解了以上内容，就可以看一下数学上的贝叶斯定理：

2.极大似然估计
  极大似然估计方法（Maximum Likelihood Estimate，MLE）也称为最大概似估计或最大似然估计，是求估计的方法之一。（还有矩估计等）
  简单来讲，极大似然估计就是给定模型，然后通过收集数据，求该模型的参数。例如，投10次特殊的硬币（给定模型），出现6次正面4次反面（请注意，这里10次结果有顺序，后面所有的投硬币结果，都有顺序）（收集数据），现在要估计投这枚硬币出现正面的概率（求参数）。
  由于提及“投硬币”，一般人的第一印象就是投到正面和反面的概率都是0.5。不过这样不利于我们接下来的学习，这里，我们需要摆脱以往的直觉，该硬币是特殊的，正反的概率并一定是0.5。
  那么，我们根据以上收集的数据先凭借直觉猜一下，很明显，由于投了10次，出现了6次正面，一般人都会猜投硬币出现正面的概率最有可能是0.6，当然也不排除其他的可能。
  而最大似然估计，简单来讲，就是用数学方法来解释你这种直觉，它就是计算出可能性最大的结果。
  上面投硬币的例子，很明显可以看出，这个模型服从二项分布，即进行多次实验，每次实验只有两种可能。用x0，x1，…，x9表示这10次投硬币的结果，用θ表示投该硬币出现正面的概率，那么把我们的直觉写成用数学写出来就是似然函数，可表示成：

  当然，不要被似然函数吓到了，他就是一个名字而已，就上面那个图片中的函数，相信你能看懂。而最大似然估计，顾名思义，就是要最大化这个似然函数，说得更简单点，就是给你一个函数，求它的极大值点。即

  对似然函数取对数，不会影响该函数的单调性，从而不会影响最后的计算的极值，也可以在一定程度上减少因计算而带来的误差，还可以极大的简化计算。
  此时求解取对数的似然函数的极大值点，就是似然函数的极大值点。由于似然函数是先单调递增，然后再单调递减的，因此，取对数的似然函数导数为0的点，即是似然函数或取对数的似然函数的极大值点（在这里也是最大值点）
  最大似然估计可以转化为求下面式子的解：

  下面简单说一下求解方法：

  这里以上面得例题为例，首先求出最大似然函数
对其进行极大似然估计
  然后对似然函数取对数，如下所示：

  最后对取对数的似然函数取进行求导，在函数的导数为0的点，即为最大似然的估计值，如下所示：

  写到这里，我们就得到了该最大似然的估计值，即投该硬币出现正面的概率θ=0.6。
  以上就是最大似然估计的方法，如果未知参数有多个，则需要用取对数的似然函数对每个参数进行求偏导，使得所有偏导均为0的值，即为该函数的极值点，一般也是其最大似然估计值。

3.最大后验概率估计
  对于最大后验概率估计，我们先进行通俗简单的理解，还是以刚才的那个问题为例，投10次硬币，结果分别是x0,x1,…,x9，出现了6次正面，4次反面。
  现在，有两个人A和B，其中A觉得那枚硬币，它就是一个一般的硬币，出现正面的概率θ = 0.5。而B觉得，它是一个特殊的硬币，出现正面的概率θ = 0.6。
  最大后验概率就是把他们的假设都进行计算（验算），然后选择其中假设最好的一个，当作最大后验概率。
  它首先计算A的假设，假设出现正面的概率θ = 0.5，那么此时，投10次该硬币，出现6次正面的概率则是

  然后再来计算一下B的假设，假设出现正面的概率θ = 0.6，那么此时，投10次该硬币，出现6次正面的概率则是

  通过计算，我们可以很直观的发现，相比于A的假设，B的假设准确的概率更大一下，当然，这里也不能说B绝对是正确的，只是B是对的可能性更大。我们一般也更相信B的猜测。
  当然，上面的例子只是对最大后验概率估计进行简单的理解。显然，我们还可以有其他假设，比如假设出现正面的概率θ = 0.7。由于θ的取值范围在0到1之间，有无数种假设，但我们不可能每种假设都进行计算，这个时候，就需要利用一些简单的数学方法，求出最大的那一个，即为最大后验概率。
  最大后验概率估计就是在已知一系列结果的情况下，求参数可能的最大的那一个，也就是求解下面式子：

  可能有人不知道为什么要写这个式子，我们来简单通俗的理解一下上面式子的含义，就是在序列x0 , x1 , … , xn已知的情况下，θ等于某个值的概率（这里不懂的，参看第一节），然后求出θ一个个的取完所有的值的所有概率，选择其中使概率最大的那一个的θ，即为最大后验概率。
  然而该式一般不能通过蛮力法直接求解，需要利用贝叶斯公式，经过一系列变换求解，过程如下：

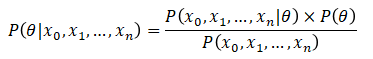
  上面这个式子中P(x0 , x1 , … , xn)表示投n次硬币，产生x0 , x1 , … , xn结果的概率，其中每个x均有两种可能，要么是正面，要么是反面。但是由于已经投了n次硬币，统计了每一次的结果，即x0 , x1 , … , xn 均已知，相当于这个事件已经发生了，所以在这里P(x0 , x1 , … , xn) = 1。
  还需要注意的是，这里的P(x0 , x1 , … , xn | θ)就是前面第二节中极大似然估计的似然函数。这里的P(θ)表示的是出现正面的概率，简单理解就是，我们最开始就需要对θ设置一个概率分布，例如可以假设它在0到1之间均匀分布，即它可以等概率的取0到1之间任意值，此时，最大后验概率估计等价于最大似然估计。假如我们不考虑太多，就觉得该硬币的出现正面的概率最接近0.5，与0.5相差越大则越不可信，那么可以将θ的概率分布假设为均值为0.5，方差为σ^2的正态分布。
  所以该题中的最大后验概率估计，也等价于下式

  对于刚才的投硬币问题，我们将θ的概率分布假设为均值为0.5，方差为1的正态分布，即θ的密度函数可表示为：

  最大后验概率的求解与最大似然估计有些类似，也是先对函数取对数，然后再求导数为0的极值点，即为最大后验估计的概率。
  具体求解过程如下：

  然后求它的极值点，即导数为0的点

在线求解一元三次方程链接

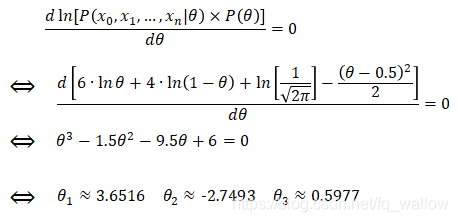
  显然在这道题中θ = 0.5977，也就是说，当θ的密度函数为均值为0.5，方差为1的正态分布时，投该硬币出现正面的概率为0.5977时是可能性最大的。
  说到这里，最大后验概率估计的方法，也差不多说完了。下面按照我所学，以容易理解的方式总结一下：
  假设你已经理解了极大似然估计，那么，最大后验的实质就是对参数的每一个可能的取值，都进行极大似然估计，并根据这个取值可能性的大小，设置极大似然估计的权重，然后选择其中最大的一个，作为最大后验估计的结果。

  注：“根据取值的可能性设置权重”：例如投硬币问题中，有人认为正面出现的概率越接近0.5越好，所以将参数取值的可能概率设置为均值为0.5，方差为1的高斯分布。