（三）从零开始学人工智能—数学基础:概率论与数理统计

最新推荐文章于 2020-08-04 20:19:46 发布

同花顺技术

最新推荐文章于 2020-08-04 20:19:46 发布

阅读量3.5k

点赞数 9

分类专栏：人工智能

本文链接：https://blog.csdn.net/weixin_45552760/article/details/101697678

版权

人工智能专栏收录该内容

19 篇文章 15 订阅

订阅专栏

概率论与数理统计

数理统计与机器学习有什么关系呢？哪些地方需要用到数理统计？

实际上，二者关心的是同一件事，即我们从数据中学到了什么。事件的概率是衡量该事件发生的可能性的量度。虽然在一次随机试验中某个事件的发生是带有偶然性的，但那些可在相同条件下大量重复的随机试验却往往呈现出明显的数量规律。
机器学习除了处理不确定量，也需处理随机量。不确定性和随机性可能来自多个方面，使用概率论来量化不确定性。概率论在机器学习中扮演着一个核心角色，因为机器学习算法的设计通常依赖于对数据的概率假设。

例如，在机器学习（Andrew Ng）的课中，会有一个朴素贝叶斯假设，就是条件独立的一个例子。该学习算法对内容做出假设，用来分辨电子邮件是否为垃圾邮件。假设无论邮件是否为垃圾邮件，单词 $x$ 出现在邮件中的概率条件独立于单词 $y$ 。很明显这个假设是非一般性的，因为某些单词几乎总是同时出现。然而，最终结果是，这个简单的假设对结果的影响并不大，且无论如何都可以让我们快速判别垃圾邮件。

拓展概括，更直白的说吧：

线性代数提供了数据的表示；
概率论与统计提供了问题的假设；
微积分提供了问题的解决方案。

目前为止，我们已经知道了数据的表示及变换等，接下来进入第二个环节，有关问题的假设，即数理统计部分。

1. 什么是统计？什么是概率？

从一个不搞笑的笑话开始吧

某次生物课考试，有一道题是看动物的脚，猜该动物的名称，一考生实在是不会做，愤怒的把试卷撕掉就往外走，老师见了，抓住他大声说道：“你哪个班的，这么嚣张”。该学生把裤腿一提，说道：“你猜呀，你猜呀”！扬长而去~

工科男就是笑点低，这也能叫做笑话~服气🎃，不管怎样，这个学生绝对是个统计高手。啊哈哈哈

辣么，统计是什么，统计就是给你一个黑盒子，里面装着猫和狗，只让你看到他们的腿，然后让你猜哪个腿是猫的：

在这里插入图片描述

你可能会问，这怎么猜？

在统计里会总结过去的数据，然后对这些数据进行总结归纳。就像刚才的例子，我们要判断出哪个腿属于猫。需要收集所有猫的腿（也就是过去的数据），然后总结这些腿的特征（总结归纳）。当图片里的腿出现时，你可以根据之前的总结归纳来判断出这腿是不是猫的腿。当然，你也不会无聊到判断哪只腿是猫，哪只腿是狗的，更多时候你可能喜欢看的是美女的腿~😍😍。

所以，统计是对过去数据进行“总结归纳”，表示如下图

在这里插入图片描述

那概率又是什么呢？

**概率是用数值来表示事情发生的可能性大小。**举个例子，小马想创业，去找投资人王思聪要钱。王思聪可不是傻X。然后就派人去调查小马过去的经历（看他有什么创业的条件），然后预测他可能成功的概率是多大。经过深入调查发现小马他爸是马云（给定条件），得出小马创业概率成功率是99%（预测未来）。

如果我们用猫和狗这个例子来举例，就是给了你猫和狗的行为特征（给定条件），然后预测猫和狗明天撕逼的可能性多大。

所以，概率是给定条件，对“数据”进行预测，可以用下图来表示：

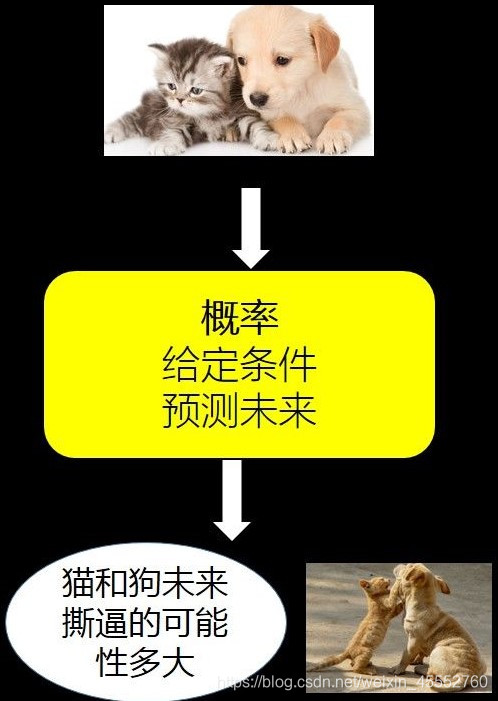
在这里插入图片描述

小结

用简单的话来总结：
统计＝回顾过去，进行归纳总结
概率＝给定条件，对未来进行预测

用稍微专业一点的话来总结：
统计＝样本(回顾过去的数据)归纳出总体(总结)
概率率＝总体(给定条件)对样本进行预测

辅助理解：

统计学：根据手中信息，猜猜桶里有啥？(样本归纳总结出总体)

概率论：根据桶中信息，猜猜手里有啥？(总体对样本进行预测)

2. 随机变量与概率分布

上文介绍了概率的本质：某件事发生的可能性。如下图

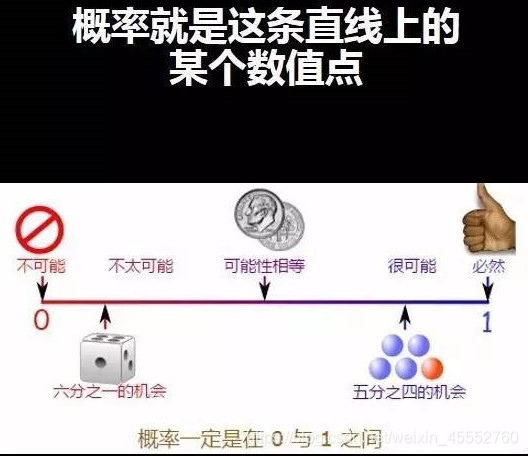
在这里插入图片描述

概率的值永远在0-1范围之间。
如果某件事不可能发生，则其概率为0，对应的就是这条直线上最左端的位置。
如果某件事肯定会发生，则其概率为1，，对应的就是这条直线上最右端的位置，也就是那个点赞的大拇指

那…怎么计算概率呢？

在网上查找前人计算的经验值。

用数据分析来计算出事件发生的数目，然后除以总数目。

关于概率的具体表现形式，还得从概率分布说起，为了搞明白什么是概率分布，还得从数据类型和分布说起，为了…，打住打住，环环相扣何时了，行吧，就从数据类型走起。

数据类型，也就是我们的随机变量，有两种：离散数据和连续数据。

随机变量（random variable）

表示随机现象（在一定条件下，并不总是出现相同结果的现象称为随机现象）中各种结果的实值函数（一切可能的样本点）。例如某一时间内公共汽车站等车乘客人数，电话交换台在一定时间内收到的呼叫次数等，都是随机变量的实例。
随机变量与模糊变量的不确定性的本质差别在于，后者的测定结果仍具有不确定性，即模糊性。

变量与随机变量的区别：

当变量的取值的概率不是1时,变量就变成了随机变量；当随机变量取值的概率为1时,随机变量就变成了变量。

比如：
当变量 $x$ 值为100的概率为1的话,那么 $x = 100$ 就是确定了的,不会再有变化,除非有进一步运算。
当变量 $x$ 的值为100的概率不为1,比如为50的概率是0.5,为100的概率是0.5,那么这个变量就是会随不同条件而变化的,是随机变量,取到50或者100的概率都是0.5,即50%。

离散数据根据名称很好理解，就是数据的取值是不连续的。例如掷硬币就是一个典型的离散数据，因为抛硬币的就2种数值（也就是2种结果，要么是正面，要么是反面）。

你可以把离散数据想象成一块一块垫脚石，你可以从一个数值调到另一个数值，同时每个数值之间都有明确的间隔。

在这里插入图片描述

连续数据正好相反，它能取任意的数值。例如时间就是一个典型的连续数据1.25分钟、1.251分钟，1.2512分钟，它能无限分割。连续数据就像一条平滑的、连绵不断的道路，你可以沿着这条道路一直走下去。

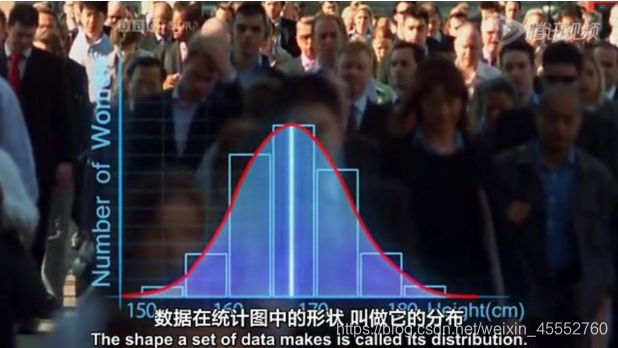
在这里插入图片描述

那什么是分布呢？

数据在统计图中的形状，叫做它的分布：

在这里插入图片描述

不好意思，楼上放错了，（冰岛雷克雅未克大教堂，其实很类似-直观），是下面这个（还不如楼上）

在这里插入图片描述

其实我们生活中也会聊到各种分布。比如~~日常“开车”的时候~~，不同季节男人的目光分布如下图（憋住，不要流鼻血）：

在这里插入图片描述

也即是

在这里插入图片描述

各位老铁，测测你目光分布在哪儿~

在这里插入图片描述

好了，美女也看了，醒醒，专心学习吧。

现在，我们已经知道了两件事：

1）数据类型（也叫随机变量）有2种：离散数据类型（例如抛硬币的结果），连续数据类型（例如时间） 2）分布：数据在统计图中的形状。

而我们的概率分布就是二者（数据类型+分布）的结合：概率分布就是在统计图中表示概率，横轴是数据的值，纵轴是横轴上对应数据值的概率。

在这里插入图片描述

很显然的，根据数据类型的不同，概率分布分为两种：离散概率分布，连续概率分布。

小结

随机变量与概率分布的联系—Part1

一个随机变量仅仅表示一个可能取得的状态，还必须给定与之相伴的概率分布来制定每个状态的可能性。用来描述随机变量或一簇随机变量的每一个可能的状态的可能性大小的方法，就是 概率分布(probability distribution).

随机变量可以分为离散型随机变量和连续型随机变量,相应的描述其概率分布的函数是:

概率质量函数(Probability Mass Function, PMF):描述离散型随机变量的概率分布，通常用大写字母 $P$ 表示。

概率密度函数(Probability Density Function, PDF):描述连续型随机变量的概率分布，通常用小写字母 $p$ 表示。

辣么，问题就来了。为什么你要关心数据类型呢？

因为数据类型会影响求概率的方法。

对于离散概率分布，我们关心的是取得一个特定数值的概率。例如抛硬币正面向上的概率为: $P (x = 正面) = 1 / 2$

而对于连续概率分布来说，我们无法给出每一个数值的概率，因为我们不可能列举每一个精确数值。

例如，你在咖啡馆约妹子出来，你提前到了。为了给妹子留下好印象，你估计妹子会在5分钟之内出现，有可能是在4分钟10秒以后出现，或者在4分钟10.5秒以后出现，你不可能数清楚所有的可能时间，你更关心的是在妹子出现前的1-5分钟内（范围），因为你想把发型重新整理下（虽然你因为加班头发已经秃顶了，但是…气质得有，发型不能乱），给妹子留个好印象。所以，对于像时间这样的连续型数据，你更关心的是一个特定范围的概率是多少。

在这里插入图片描述

小结

随机变量与概率分布的联系—Part2

1.离散型随机变量和概率质量函数

PMF 将随机变量能够取得的每个状态映射到随机变量取得该状态的概率。

一般而言， $P (x)$ 表示时 $X = x$ 的概率.
有时候为了防止混淆，要明确写出随机变量的名称 $P ($ x $= x)$
有时候需要先定义一个随机变量，然后制定它遵循的概率分布x服从 $P ($ x $)$

PMF 可以同时作用于多个随机变量，即**联合概率分布(joint probability distribution) ** $P (X = x, Y = y)$ *表示 $X = x$ 和 $Y = y$ 同时发生的概率，也可以简写成 $P (x, y)$ .

如果一个函数 $P$ 是随机变量 $X$ 的 PMF，那么它必须满足如下三个条件

$P$ 的定义域必须是的所有可能状态的集合
$\forall x \in$ x, $\leq P(x) \leq 1$ .
$_{x∈X} P(x)=1$ . 我们把这一条性质称之为归一化的(normalized)

2.连续型随机变量和概率密度函数

如果一个函数 $p$ 是x的PDF，那么它必须满足如下几个条件

$p$ 的定义域必须是 x 的所有可能状态的集合。
$\forall x \in X, p (x) \geq 0$ . 注意，我们并不要求 $p (x) \leq 1$ ，因为此处 $p (x)$ 不是表示的对应此状态具体的概率，而是概率的一个相对大小(密度)。具体的概率，需要积分去求。
$\int p (x) d x = 1$ , 积分下来，总和还是1，概率之和还是1.

注：PDF $p (x)$ 并没有直接对特定的状态给出概率，给出的是密度，相对的，它给出了落在面积为 $δ x$ 的无线小的区域内的概率为 $p (x) δ x$ . 由此，我们无法求得具体某个状态的概率，我们可以求得的是某个状态 $x$ 落在某个区间 $[a, b]$ 内的概率为 $\int_{a}^{b}p(x)dx$ .

概率分布是怎么得出来的呢？

当统计学家们开始研究概率分布时，他们看到，有几种形状反复出现，于是就研究他们的规律，根据这些规律来解决特定条件下的问题。几种经常出现的形状就是就是日常常见的几种特殊分布。

这些特殊分布有什么用呢？回想一下高考的时候，准备的那几篇英语作文“万能模板”，虽然你最后也没用上吧😂😹，但是万一呢，岂不是爽翻！

2.2.3 常见概率分布

接下里我们就聊聊几种常见的分布。

3种离散概率分布：二项分布，泊松分布，几何分布
1种连续概率分布：正态分布

介绍之前，提前引入两个知识点：

期望：概率的平均值

标准差：衡量数据的波动大小

二项分布

预期解决以下三个问题：

1.二项分布有啥用？ 2.如何判断是不是二项分布？ 3.二项分布如何计算概率？

二项分布有啥用？

当你遇到一个事件，如果该事件发生次数固定，而你感兴趣的是成功的次数，那么就可以用二项分布的公式快速计算出概率来。

比如，你5家公司的股票（谷歌，Facebook，苹果，阿里巴巴，腾讯），为了保底和计算投入进去多少钱，你想知道其中3只股票帮你赚到钱（成功的次数）的概率多大，那么这时候就可以用二项分布计算出来。

在这里插入图片描述

如何判断是不是二项分布？

首先，为啥叫二项，不叫三项，或者二愣子呢？故明思义，二项代表事件有2种可能的结果，把一种称为成功，另外一种称为失败。生活中有很多这样2种结果的二项情况，例如，你表白是二项的，一种成功，一种是失败。

那满足什么条件可判断事件符合二项分布呢？只要符合下面几个特点就可以判断某事件是二项分布了：

做某件事的次数（也叫试验次数）是固定的，用n表示。

例如，抛硬币3次，投资5支股票。

每一次事件都有两个可能的结果（成功，或者失败）

例如，每一次抛硬币有2个结果：正面表示成功，反面表示失败。每一次投资美股有2个结果：投资成功，投资失败。

每一次成功的概率都是相等的，成功的概率用p表示

例如，每一次抛硬币正面朝上的概率都是1/2。你投资了5家公司的股票，假设每一家投资盈利成功的概率都相同。

你感兴趣的是成功 $x$ 次的概率是多少。那么就可以用二项分布的公式快速计算出来了。

例如，你已经知道了前面讲的5家美股的赚钱概率最大，所以你买了这5家公司的股票，假设投资的这5家公司成功的概率都相同，那么你关心其中只要有3个投资成功，你就可以赚翻了，所以想知道成功3次的概率。

根据这几个特点，我们就知道抛硬币是一个典型的二项分布，还有你投资的这5支股票也是一个典型的二项分布（在假设每家公司投资成功的前提下）。

二项分布如何计算概率？

怎么计算符合二项分布事件的概率呢？例如：你抛硬币3次，2次正面朝上的概率是多少？你买了这5家公司的股票，3支股票赚钱的概率是多大？

根据特点中的符号表示，可通过如下公式进行计算：

$P(x)=C^x_np^x(1-p)^{n-x} \tag{1}$ , 其中 $n$ 为事件发生次数，而 $x$ 为成功的次数。

例如，抛硬币5次（ $n$ ），恰巧有3次正面朝上（ $x = 3$ ，抛硬币正面朝上概率 $p = 1 / 2$ ），可以用式(1)计算出概率为31.25%。

二项分布的期望与标准差

期望： $E (x) = n p$ ，表示某事件发生 $n$ 次，预期成功多少次。

标准差： $\sigma(x)=\sqrt{np(1-p)}$ ，表示数据波动大小

知道这个期望有啥用呢？

做任何事情之前，知道预期结果肯定对你后面的决策有帮助。比如你抛硬币5次，每次概率是 $1 / 2$ ，那么期望 $E (x) = 5 * 1 / 2 = 2.5$ 次，也就是有大约3次你可以抛出正面。

再比如你之前投资的那5支股票，假设每支股票帮你赚到钱的概率是80%，那么期望 $E(x)=5*80\%=4$ ，也就是预期会有4只股票投资成功帮你赚到钱。

几何分布

其实我一直把几何分布，叫做二项分布的孪生兄弟，因为他两太像了。只有一点不同，就像海尔兄弟只有内裤不同一样。

在这里插入图片描述

我们还是从下面这个套路聊起来一起找出这个不同的“劲爆点”：

1.几何分布有啥用？ 2.如何判断是不是几何分布？ 3.几何分布如何计算概率？

几何分布有啥用？

如果你想知道尝试多少次能取得第一次成功的概率，则需要几何分布。

如何判断是不是几何分布？

只要符合下面几个特点就可以判别事件符合几何分布了：

做某事件次数（也叫试验次数）是固定的，用n表示

例如，抛硬币3次，表白5次

每一次事件都有两个可能的结果（成功，或者失败）

例如，每一次抛硬币有2个结果：正面表示成功，反面表示失败。每一次表白有2个结果：表白成功，表白失败。

每一次“成功”的概率都是相等的，成功的概率用p表示

例如，每一次抛硬币正面朝上的概率都是1/2。假设你是初出茅庐的小伙子，还不是老油条，所以你表白每一次成功的概率是一样的。

你感兴趣的是，进行x次尝试这个事情，取得第1次成功的概率是多大

例如，你在玩抛硬币的游戏，想知道抛5次硬币，只有第5次（就是第1次成功）正面朝上的概率是多大。你表白你的暗恋对象，你希望知道要表白3次，心仪对象答应和你手牵手的概率多大（第一次成功之后就没有后续了）。

从中可以看出，几何分布与二项分布只有最后一点，也就是解决问题的目的不同。

几何分布如何计算概率？

计算公式如下：

$P(x)=(1-p)^{x-1}p$ ，其中 $p$ 为每次成功的概率，即为了在第 $x$ 尝试后取得第1次成功，首先你要失败 $x - 1$ 次。

假如在表白之前，你计算出即使你尝试表白3次，在最后1次成功的概率还是小于50%，还没有抛硬币的概率高，那你就要考虑换个追求对象；或者首先提升下自己，提高自己每一次表白的概率，比如，下班后晚上去做个头发呀😝😝

几何分布的期望与标准差

期望： $E (x) = 1 / p$

标准差： $\sigma(x)=(1-p)p^2$

知道这个期望有啥用呢？

假如你每次表白的成功概率是60%，同时你也符合几何分布的特点，期望: $E (x) = 1 / p = 1 / 0.6 = 1.67$ ，这意味着什么？意味着极有可能一次成功不了😂

但是，你可以期望自己表白1.67次（约等于2次）会成功，这是不是让你信心倍增，起码你不需要努力上100次才能成功，2次还是能做到的，有必要尝试下。

泊松分布

还是同样的套路，从以下几个方面入手：

1.泊松分布有啥用？ 2.如何判断是不是泊松分布？ 3.泊松分布如何计算概率？

泊松分布有啥用？

如果你想知道某个时间范围内，发生某件事情 $x$ 次的概率是多大。这时候就可以用泊松分布轻松搞定。比如一天内中奖的次数，一个月内某机器损坏的次数等。

*知道这些事情的概率有啥用呢？*当然是根据概率的大小来做出决策了。

比如，你搞了个抽奖活动，最后算出来一天内中奖10次的概率都超过了90%，然后你顺便算了下期望，再和你的活动成本比一下，发现要赔不少钱，那这个活动就别瞎搞了。

泊松分布的形状会随着平均值的不同而有所变化，无论是一周内多少人能赢得彩票，还是每分钟有多少人会打电话到呼叫中心，泊松分布都可以告诉我们它们的概率。

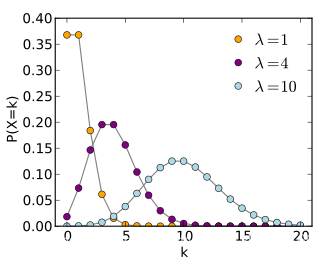
在这里插入图片描述

如何判断是不是泊松分布？

事件是独立事件

对于事件 $A$ 与事件 $B$ ，如果 $P (A B) = P (A) P (B)$ ，则事件 $A$ 与事件 $B$ 独立。类似于抽奖这类的就是独立事件。

在任意相同的时间范围内，事件发的概率相同

例如，1天内中奖概率，与第2天内中奖概率相同。

你想知道某个时间范围内，发生某件事情 $x$ 次的概率是多大

例如，你搞了个促销抽奖活动，想知道一天内10人中奖的概率。

泊松分布如何计算概率？

计算公式如下：

$P(x)=\frac{u^xe^{-u}}{x!}$ ，其中 $x$ 代表事件发生次数（例如10个人中奖）， $u$ 代表给定时间范围内事件发生的平均次数（例如你搞的抽奖活动1天平均中奖人数是5人）。

例如，你搞了个促销抽奖活动，只知道1天内中奖的平均个数为5个，你想知道1天内恰巧中奖次数为7的概率是多少？

此时 $x = 7 ， u = 5$ （区间内发生的平均次数），代入公式求出概率为10.44%。

泊松分布的期望与标准差

期望： $E (x) = u$

标准差： $\sigma(x)=u$

正态分布

上述分布都是离散概率分布，当随机变量是连续型时，情况就完全不一样了。因为离散概率的本质是求x取某个特定值的概率，而连续随机变量不行，它的取值是可以无限分割的，它取某个值时概率近似于0。连续变量是随机变量在某个区间内取值的概率，此时的概率函数叫做概率密度函数。

正态概率分布(The Normal Distribution)，也叫高斯分布(Gaussian Distribution)，是连续型随机变量中最重要的分布。世界上绝大部分的分布都属于正态分布，人的身高体重、考试成绩、降雨量等都近似服从。

为什么叫正太分布，我也不理解，因为英文单词“Normal”意思是“常见的，典型的”，不应该叫常态分布么😂😹（湾湾好像就是这么翻译的😶😶）

正态分布如同一条钟形曲线。中间高，两边低，左右对称。想象身高体重、考试成绩，是否都呈现这一类分布态势：大部分数据集中在某处，小部分往两端倾斜。

正太概率密度函数为：

$f(x;\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}}e^{-(x-\mu)^2/2\sigma^2} \tag{2}$

其中， $\mu$ 代表均值， $\sigma$ 代表标准差，不同的取值将会形成不同形状的正态分布。均值决定分布的左右偏移，标准差决定分布曲线的宽度和平坦，值越大曲线越平坦。如下图所示，正态随机变量有69.3%的值在均值加减一个标准差的范围内，95.4%的值在两个标准差内，99.7%的值在三个标准差内。这条经验法则可以帮助我们快速计算数据的大体分布。

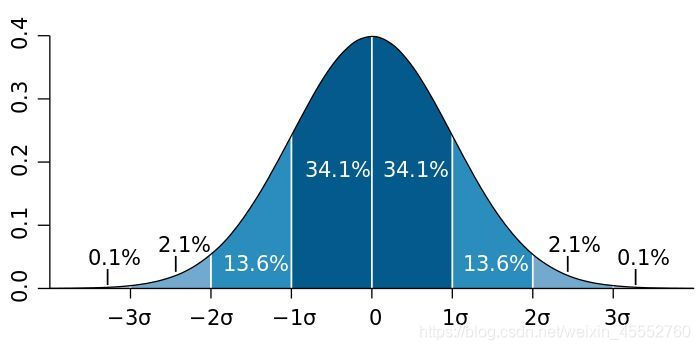
在这里插入图片描述

当均值 $\mu=0$ ，标准差 $\sigma=1$ 时，正态分布被叫做标准正态分布。它的随机变量用 $z$ 表示，它是统计推理的基础。并可进一步简化公式：

$f(z)=\frac{1}{\sqrt{2\pi}}e^{-z^2/2}$

现在可以使用简化的公式计算概率密度了，为什么这么说呢，因为所有的正态分布都可以转换为标准正态分布，只需 $z=(x-\mu)/\sigma$ 即可。

何时采用正态分布？

缺乏实数上分布的先验知识, 不知选择何种形式时, 默认选择正态分布总是不会错的, 理由如下:

中心极限定理告诉我们, 很多独立随机变量均近似服从正态分布, 现实中很多复杂系统都可以被建模成正态分布的噪声, 即使该系统可以被结构化分解。
正态分布是具有相同方差的所有概率分布中, 不确定性最大的分布, 换句话说, 正态分布是对模型加入先验知识最少的分布。

概率分布扩展

Bernoulli分布

Bernoulli分布是单个二值随机变量分布, 单参数 $\phi$ ∈[0,1]控制, $\phi$ 给出随机变量等于1的概率. 主要性质有:
$\begin{aligned}P(x=1) &= \phi \\P(x=0) &= 1-\phi \\P(x=x) &= \phi^x(1-\phi)^{1-x} \\\end{aligned}$
其期望和方差为:
$\begin{aligned} E_x[x] &= \phi \\ Var_x(x) &= \phi{(1-\phi)} \end{aligned}$
Multinoulli分布也叫范畴分布, 是单个k值随机分布,经常用来表示对象分类的分布. 其中 $k$ 是有限值.Multinoulli分布由向量 $\vec{p}\in[0,1]^{k-1}$ 参数化,每个分量 $p_i$ 表示第 $i$ 个状态的概率, 且 $p_k=1-1^Tp$ .

适用范围: 伯努利分布适合对离散型随机变量建模.

指数分布

深度学习中, 指数分布用来描述在 $x = 0$ 点处取得边界点的分布, 指数分布定义如下:
$p(x;\lambda)=\lambda I_{x\geq 0}exp(-\lambda{x}) \tag{3}$
指数分布用指示函数 $I_{x\geq 0}$ 来使 $x$ 取负值时的概率为零。

Laplace 分布

一个联系紧密的概率分布是 Laplace 分布（Laplace distribution），它允许我们在任意一点 $\mu$ 处设置概率质量的峰值
$Laplace(x;\mu;\gamma)=\frac{1}{2\gamma}exp\left(-\frac{|x-\mu|}{\gamma}\right) \tag{4}$
Dirac分布和经验分布

Dirac分布可保证概率分布中所有质量都集中在一个点上. Diract分布的狄拉克 $\delta$ 函数(也称为单位脉冲函数)定义如下:
$p(x)=\delta(x-\mu), x\neq \mu \tag{5}$

$\int_{a}^{b}\delta(x-\mu)dx = 1, a < \mu < b \tag{6}$

Dirac 分布经常作为经验分布（empirical distribution）的一个组成部分出现
$\hat{p}(\vec{x})=\frac{1}{m}\sum_{i=1}^{m}\delta(\vec{x}-{\vec{x}}^{(i)}) \tag{7}$
, 其中, m个点 $x^{1},...,x^{m}$ 是给定的数据集, 经验分布将概率密度 $\frac{1}{m}$ 赋给了这些点.

当我们在训练集上训练模型时, 可以认为从这个训练集上得到的经验分布指明了采样来源.

适用范围: 狄拉克δ函数适合对连续型随机变量的经验分布.

2.2.4 联合概率、边缘概率、条件概率

联合概率

联合概率指的是包含多个条件且所有条件同时成立的概率，记作 $P (X = a, Y = b)$ 或 $P (a, b)$ 。代表在多元的概率分布中多个随机变量分别满足各自条件的概率。

边缘概率

边缘概率是与联合概率对应的， $P (X = a)$ 或 $P (Y = b)$ ，这类仅与单个随机变量有关的概率称为边缘概率。

联合概率与边缘概率关系

联合分布可求边缘分布，但若只知道边缘分布，无法求得联合分布。

$P(X=a)=\sum_{b}P(X=a,Y=b) \tag{8}$

$P(X=b)=\sum_{a}P(X=a,Y=b) \tag{9}$
求和符号表示穷举所有 $Y$ （或 $X$ ）所能取的 $b$ （或 $a$ ）后，所有对应值相加得到的和。

条件概率

条件概率表示在条件 $Y = b$ 成立的情况下， $X = a$ 的概率，记作 $P (X = a ∣ Y = b)$ 或 $P (a ∣ b)$ ，它具有如下性质：
“在条件 $Y = b$ 下 $X$ 的条件分布”也是一种“ $X$ 的概率分布”，因此穷举 $X$ 的可取值之后，所有这些值对应的概率之和为1即：
$\sum_{a}P(X=a|Y=b)=1 \tag{10}$

条件概率例子：条件概率文氏图示意

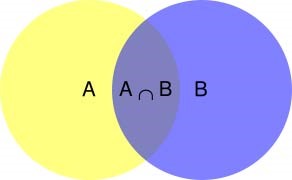
在这里插入图片描述

根据文氏图，可以很清楚地看到在事件B发生的情况下，事件A发生的概率就是 $P(A\bigcap B)$ 除以 $P (B)$ ：

$P(A\cap B) / P(B) \tag{11}$

可以这样解释：在同一个样本空间 $\Omega$ 中的事件或者子集 $A$ 与 $B$ ，如果随机从 $\Omega$ 中选出的一个元素属于 $B$ ，那么下一个随机选择的元素属于 $A$ 的概率就定义为在 $B$ 的前提下 $A$ 的条件概率。

联合概率、边缘概率与条件概率之间的关系

借用上面例子的图示，有

$\frac{P(X=A,Y=B)}{P(Y=B)} \tag{12}$

将概率从面积的角度来看：

联合概率 $P (X = A, Y = B)$
满足 $X = A$ 且 $Y = B$ 的面积
边缘概率 $P (X = A)$
不考虑 $Y$ 的取值，所有满足 $X = A$ 的区域的总面积
条件概率 $P (X = A ∣ Y = B)$
在 $Y = B$ 的前提下，满足 $X = A$ 的面积（比例）

**思考：**联合概率、边缘概率、条件概率与贝叶斯的关系？

多说一点：条件概率的链式法则

什么是条件概率的链式法则，直白点就是条件概率的推广。

由条件概率的定义，可直接得出下面的乘法公式：
乘法公式设 $A, B$ 是两个事件，并且 $P (A) > 0$ , 则有
$\tag{13}$
推广
$\tag{14}$
一般地，用归纳法可证：若 $P(A_1A_2...A_n)>0$ ，则有
$P(A_1A_2...A_n)=P(A_n|A_1A_2...A_{n-1})P(A_{n-1}|A_1A_2...A_{n-2})...P(A_2|A_1)P(A_1)=P(A_1)\prod_{i=2}^{n}P(A_i|A_1A_2...A_{i-1}) \tag{15}$
任何多维随机变量联合概率分布，都可以分解成只有一个变量的条件概率相乘形式。

补充：独立性和条件独立性

独立性
两个随机变量 $X$ 和 $Y$ ，概率分布表示成两个因子乘积形式，一个因子只包含 $X$ ，另一个因子只包含 $Y$ ，两个随机变量相互独立(independent)。
条件有时为不独立的事件之间带来独立，有时也会把本来独立的事件，因为此条件的存在，而失去独立性。
举例： $P (X Y) = P (X) P (Y)$ , 事件 $X$ 和事件 $Y$ 独立。此时给定 $Z$ ，
$\not = P(X|Z)P(Y|Z) \tag{16}$
事件独立时，联合概率等于概率的乘积。这是一个非常好的数学性质，然而不幸的是，无条件的独立是十分稀少的，因为大部分情况下，事件之间都是互相影响的。

条件独立性
给定 $Z$ 的情况下, $X$ 和 $Y$ 条件独立，当且仅当
$X\bot Y|Z \iff P(X,Y|Z) = P(X|Z)P(Y|Z) \tag{17}$
$X$ 和 $Y$ 的关系依赖于 $Z$ ，而不是直接产生。

**举例：**定义如下事件：
$X$ ：明天下雨；
$Y$ ：今天的地面是湿的；
$Z$ ：今天是否下雨；
$Z$ 事件的成立，对 $X$ 和 $Y$ 均有影响，然而，在 $Z$ 事件成立的前提下，今天的地面情况对明天是否下雨没有影响。

2.2.5 全概率、贝叶斯理解

1） 全概率公式

基本思想是：先化整为零，再聚零为整。

从一个例子入手：
人的性别由一对染色体决定：男性为XY，女性为XX，每个人从父母处各得到一个性染色体，色盲基因由X染色体携带，依此，若男性的X染色体有此基因则男性患色盲，女性则要两个X染色体均由此基因才患色盲，而两个染色体是否有色盲基因是独立的。设色盲基因出现的概率是0.08，男女婴出生比例为110:100。问一新生儿有色盲的概率是多少？

设“新生儿有色盲”为事件A，则目标概率为 $P (A)$ ，记 $B_1$ 表示“男婴”， $B_2$ 表示“女婴”，则有：

$P(B_1)=\frac{110}{110+100}=\frac{1.1}{1.1+1}$
$P(A|B_1)=0.08$
$P(A|B_2)=0.08 * 0.08=0.0064$

$P(B_1)=\frac{110}{110+100}=\frac{1.1}{1.1+1}$
$P(B_2)=\frac{100}{110+100}=\frac{1}{1.1+1}$
$P(A|B_1)=0.08$
$P(A|B_2)=0.08 * 0.08=0.0064$

进一步地，加权平均，则

$P(A)=P(B_1) * P(A|B_1)+P(B_2) * P(A|B_2)=0.08*\frac{1.1}{1.1+1}+0.0064*\frac{1}{1.1+1}=0.045$

在这个例子中， $B_1$ 和 $B_2$ 是互斥事件，即，不可能出现既是男性又是女性的情况，并且这些互斥事件对样本空间是完备的（ $B_1$ 并 $B_2$ =样本空间），也就是说除了这两种性别，这个样本空间里没有其他性别了。现有另外一个事件A（新生儿有色盲），我们可以很容易理解，在 $B_1$ 发生下 $A$ 发生和在 $B_2$ 发生下 $A$ 发生包含了所有 $A$ 发生的情况，也即是，男性婴儿患色盲与女性婴儿患色盲加和就是所有婴儿患色盲的情况。

一般性情况如下图所示：
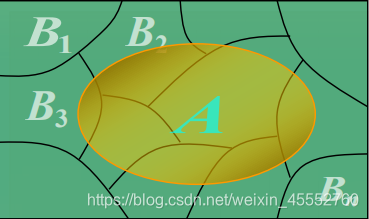
在这里插入图片描述

如图， $B_1,B_2,B_3,\cdots,B_n$ 互斥（没有交叠），且构成了样本空间的完备集。则计算A发生概率的步骤为：

先化整为零计算 $P(A|B_i),i=1,2,\cdots,n$
再聚零为整计算 $P(A|B_i)P(B_i)+\cdots+P(A|B_n)P(B_n)$

得到全概率公式：

$P(A)=\sum _{i=1}^nP(A|B_i)P(B_i)\tag{18}$

全概率公式通过划分 $\left \{ B_i \mid i=1...n \right \}$ 来计算一个事件 $A$ 的概率,更重要的是，有时候需要弄清楚在 $A$ 发生的条件下，每个 $B_i$ 发生的条件概率。即反过来考虑，这个新生儿患有色盲，那它是男性或女性的概率分别是多少。这就是我们的贝叶斯解决的问题。

2） 贝叶斯定理

简介

贝叶斯定理是18世纪英国数学家托马斯·贝叶斯（Thomas Bayes）提出得重要概率论理论。以下摘一段 wikipedia 上的简介：

所谓的贝叶斯定理源于他生前为解决一个“逆概”问题写的一篇文章，而这篇文章是在他死后才由他的一位朋友发表出来的。在贝叶斯写这篇文章之前，人们已经能够计算“正向概率”，如“假设袋子里面有 N 个白球，M 个黑球，你伸手进去摸一把，摸出黑球的概率是多大”。而一个自然而然的问题是反过来：“如果我们事先并不知道袋子里面黑白球的比例，而是闭着眼睛摸出一个（或好几个）球，观察这些取出来的球的颜色之后，那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。这个问题，就是所谓的逆向概率问题。

贝叶斯定理的思想出现在18世纪，但真正大规模派上用途还得等到计算机的出现。因为这个定理需要大规模的数据计算推理才能凸显效果，它在很多计算机应用领域中都大有作为，如自然语言处理，机器学习，推荐系统，图像识别，博弈论等等。

定义

贝叶斯定理是关于随机事件A和B的条件概率：

$P(A|B)=\frac{P(B|A)P(A)}{P(B)} \tag{19}$

其中 $P (A ∣ B)$ 是在 $B$ 发生的情况下 $A$ 发生的可能性。在贝叶斯定理中，每个名词都有约定俗成的名称：

$P (A)$ 是 $A$ 的先验概率，之所以称之为“先验”，是因为它不考虑任何 $B$ 的事件的因素；
$P (A ∣ B)$ 是已知 $B$ 发生后 $A$ 的条件概率，也由于得自 $B$ 的取值而被称作 $A$ 的后验概率。
$P (B ∣ A)$ 是已知 $A$ 发生后 $B$ 的条件概率，也由于得自 $A$ 的取值而被称作 $B$ 的后验概率。
$P (B)$ 是 $B$ 的先验概率，也作标淮化常量（normalizing constant）。

推导

我们可以从条件概率的定义推导出贝叶斯定理。
根据条件概率的定义，在事件 $B$ 发生的条件下条件 $A$ 发生的概率为：

$P(A|B)=\frac{P(A\cap B)}{P(B)} \tag{20}$ ，其中 $P(A\cap B)$ 为 $A, B$ 的联合概率。

同样地，在事件 $A$ 发生的条件下事件 $B$ 发生的概率为：

$P(B|A)=\frac{P(A\cap B)}{P(A)} \tag{21}$ ，其中 $P(A\cap B)$ 为 $A, B$ 的联合概率。

结合式(20)和式(21)，可以得到：

$P(A|B)P(B)=P(A\cap B)=P(B|A)P(A) \tag{22}$

这个引理有时称作概率乘法规则。上式两边同除以 $P (B)$ ，若 $P (B)$ 是非零的，我们可以得到贝叶斯定理:

$P(A|B)=\frac{P(B|A)P(A)}{P(B)} \tag{23}$

解释

通常，事件 $A$ 在事件 $B$ 发生的条件下的概率，与事件 $B$ 在事件 $A$ 发生的条件下的概率是不一样的；然而，这两者是有确定关系的，贝叶斯定理就是这种关系的陈述。

贝叶斯公式的用途在于通过己知三个概率来推测第四个概率。它的内容是：在 $B$ 出现的前提下， $A$ 出现的概率等于 $A$ 出现的前提下 $B$ 出现的概率乘以 $A$ 出现的概率再除以 $B$ 出现的概率。通过联系 $A$ 与 $B$ ，计算从一个事件发生的情况下另一事件发生的概率，即从结果上溯到源头（也即逆向概率）。

通俗地讲就是当你不能确定某一个事件发生的概率时，你可以依靠与该事件本质属性相关的事件发生的概率去推测该事件发生的概率。用数学语言表达就是：支持某项属性的事件发生得愈多，则该事件发生的的可能性就愈大。这个推理过程有时候也叫贝叶斯推理。

示例

已知男性中有5%是色盲患者，女性中有0.25%是色盲患者，现从男女比例为20:180的人群中随机地挑选一个人，发现恰好是色盲患者，问此人是男性的概率大还是女性的概率大。
　　解答：
　　记 $A$ 表示为色盲患者；记 $B_1$ 表示问男性， $B_2$ 表示为女性,则:

$P(B_1)=\frac{20}{20+180}=\frac{1}{10}$
$P(B_2)=\frac{180}{20+180}=\frac{9}{10}$
$P(A|B_1)=0.05$
$P(A|B_2)=0.0025$
$P(A)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)$

由贝叶斯公式(40)可得：
　　该色盲患者是男性的概率是： $P(B_1|A)=\frac{P(A|B_1)P(B_1)}{P(A)}=0.69$
　　该色盲患者是女性的概率是： $P(B_2|A)=\frac{P(A|B_2)P(B_2)}{P(A)}=0.31$
　　由于 $0.69 > 0.31$ ，从而可得该色盲患者是男性的概率比较大。

小结

以上基本为我们的概率论部分，下面为数理统计部分。

2.2.6 期望、方差、协方差、相关系数

1）期望

其实上文已经多次提到了期望，这里正式定义一番：在概率与数理统计中，数学期望（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和。它反映随机变量平均取值的大小。

性质：

线性运算： $E (a X + b Y + c) = a E (X) + b E (Y) + c$
推广形式： $E(\sum_{k=1}^{n}{a_iX_i+c}) = \sum_{k=1}^{n}{a_iE(X_i)+c}$

函数期望：设设 $f (x)$ 为 $x$ 的函数，则 $f (x)$ 的期望为

离散函数： $E(f(x))=\sum_{k=1}^{n}{f(x_k)P(x_k)}$
连续函数： $E(f(x))=\int_{-\infty}^{+\infty}{f(x)p(x)dx}$

注意：

函数的期望大于等于期望的函数（ $J e n s e n$ 不等式），即 $E(f(x))\geqslant f(E(x))$
一般情况下，乘积的期望不等于期望的乘积。
如果 $X$ 和 $Y$ 相互独立，则 $E (X Y) = E (X) E (Y)$ 。

2）方差

概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。方差是一种特殊的期望。定义为：
$E((X-E(X))^2) \tag{23}$

方差性质：

1） $Var(X) = E(X^2) -E(X)^2$
2）常数的方差为0;
3）方差不满足线性性质;
4）如果 $X$ 和 $Y$ 相互独立, $Var(aX+bY)=a^2Var(X)+b^2Var(Y)$

前文提到的标准差，是方差的算术平方根，即 $\sigma=\sqrt{Var(X)}$ 。

3） 协方差

协方差是衡量两个变量线性相关性强度及变量尺度。两个随机变量的协方差定义为：
$\tag{24}$
方差是一种特殊的协方差。当 $X = Y$ 时， $C o v (X, Y) = V a r (X) = V a r (Y)$ 。

协方差性质：

1）独立变量的协方差为0。
2）协方差计算公式：

$Cov(\sum_{i=1}^{m}{a_ix_i}, \sum_{j=1}^{m}{b_jy_j}) = \sum_{i=1}^{m} \sum_{j=1}^{m}{a_ib_jCov(x_iy_i)} \tag{25}$

3）特殊情况：

$\tag{26}$

4） 相关系数

相关系数是研究变量之间线性相关程度的量。两个随机变量的相关系数定义为：

$\frac{Cov(x,y)}{\sqrt{Var(x)Var(y)}} \tag{27}$

相关系数的性质：
1）有界性。相关系数的取值范围是 $[- 1, 1]$ ，可以看成无量纲的协方差。
2）值越接近1，说明两个变量正相关性（线性）越强。越接近-1，说明负相关性越强，当为0时，表示两个变量没有相关性。

2.2.7 参数估计

统计学方法包括统计描述和统计推断两种方法，其中，推断统计又包括参数估计和假设检验。上文介绍了基本的统计描述，本节将介绍常用参数估计。

参数估计就是用样本统计量去估计总体的参数的真值，它的方法有点估计和区间估计两种。

点估计就是直接以样本统计量直接作为相应总体参数的估计值。点估计的缺陷是没法给出估计的可靠性，也没法说出点估计值与总体参数真实值接近的程度。

区间估计是在点估计的基础上给出总体参数估计的一个估计区间，该区间是由样本统计量加减允许误差（极限误差）得到的。在区间估计中，由样本统计量构造出的总体参数在一定置信水平下的估计区间称为置信区间。

在其它条件相同的条件下，区间估计中置信度越高，置信区间越大。置信水平为1-a, a（显著性水平）为小概率事件或者不可能事件，常用的置信水平值为99%，95%，90%，对应的a为0.01, 0.05， 0.1

1）最大似然估计、最大后验估计、贝叶斯估计

在这里插入图片描述

2）上文提到推断统计包括参数估计和假设检验，那剩下的假设检验就留给大家思考

假设检验与参数估计之间的相同点、联系与区别？

声明

本博客所有内容仅供学习，不为商用，如有侵权，请联系博主谢谢。

参考文献

[1] 盛骤，试式千，潘承毅等编. 概率论与数理统计（第4版）[M]，高等教育出版社，2008
[2] 猴子聊机器学习
[3] Jim Liang， Getting Started with Machine Learning，2018
[4] 周志华.机器学习[M].清华大学出版社，2016.
[5] Ian，Goodfellow，Yoshua，Bengio，Aaron…深度学习[M]，人民邮电出版，2017
[6] WikiPedia贝叶斯定理
[7] Mbalib贝叶斯法则
[8] 刘伟鹏，数学之美番外篇：平凡而又神奇的贝叶斯方法

同花顺技术

关注

9
点赞
踩
41

收藏

觉得还不错? 一键收藏
2
评论
（三）从零开始学人工智能—数学基础:概率论与数理统计

概率论与数理统计数理统计与机器学习有什么关系呢？哪些地方需要用到数理统计？实际上，二者关心的是同一件事，即我们从数据中学到了什么。事件的概率是衡量该事件发生的可能性的量度。虽然在一次随机试验中某个事件的发生是带有偶然性的，但那些可在相同条件下大量重复的随机试验却往往呈现出明显的数量规律。机器学习除了处理不确定量，也需处理随机量。不确定性和随机性可能来自多个方面，使用概率论来量化不确定性。 ...
复制链接

扫一扫