
概述
提起字符串匹配可能更多人会想到 KMP 算法,该算法时间复杂度为 O(m+n),而且也是我们在学习数据结构过程中最早接触到的比较好的算法。但 KMP 算法需要在模式字符串有关联的情况下,也即模式字符串前后缀字符相似度较高的情况下匹配效率比较高。但是在实际应用场景中模式字符串更多情况下是无规律的,因此在工程应用中字符串匹配问题的解决更多的使用的是 sunday 算法。
解题思路
sunday 算法较之于 BM 算法最大的不同点在于 sunday 算法在匹配的过程中主串中参加匹配的最末位字符的下一位字符。
- 如果末尾的下一位字符(如该字符为'a')没有在模式字符串中出现过,则直接跳到'a'的下一位字符开始新一轮的比较
- 如果模式字符串中包含'a',则将模式字符串中从左到右中最早出现的字符'a'与源字符串中的'a'对应开始新一轮的匹配
我们下边举一个例子来说明 sunday 算法的匹配过程。比如在一个主串"substring searching"中查找模式串"search"。
- 开始时,将模式字符串和主字符串左侧对齐开始进行匹配
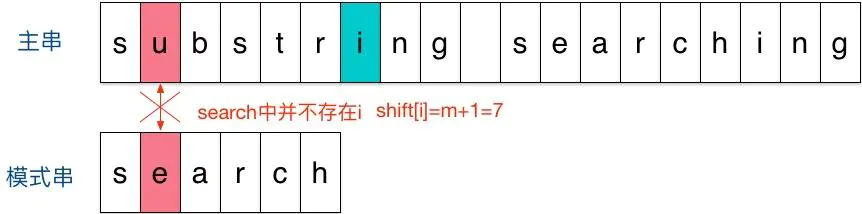
- 在匹配的过程中发现在第二个字符
e处出现匹配失败的情况。此时我们关注参与匹配的最末尾字符的下一位即i,由于模式字符串中并没有i,因此模式字符串直接跳过一大片,向右移动位数=模式字符串长度 +1,也即移动到字符n的位置。
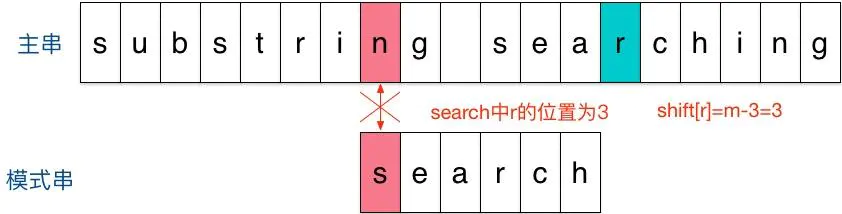
- 在新一轮的匹配过程中发现第一个字符便出现了不匹配的情况。然后我们看到参与匹配的末尾字符的下一位字符为
r,并且r存在于模式字符串中因此可以将模式字符串移动 3 位(移动到模式字符串中的r和主字符串中的r对齐)如下:
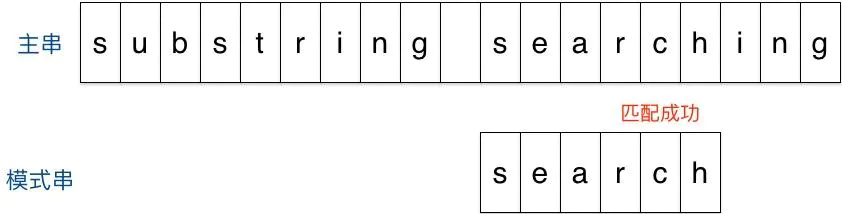
- 在新一轮匹配过程中发现匹配成功,结束匹配返回匹配的位置。
代码
class Solution {
//使用sunday算法来求解
public int strStr(String haystack, String needle) {
//边界判断
if(needle.equals("")||needle==null){
return 0;
}
if(haystack==null){
return -1;
}
char [] haystackArray=haystack.toCharArray();
char []needleArray=needle.toCharArray();
int haystackLength=haystackArray.length;
int needleLength=needleArray.length;
//定义偏移数组
int move[]=new int[256];
//对偏移数组进行初始化工作
for(int i=0;i<256;i++){
move[i]=needleLength+1;
}
for(int i=0;i<needleLength;i++){
move[needleArray[i]]=needleLength-i;
}
//模式字符串第一个字符在匹配过程与源字符串对应的未知,j表示当前已经匹配的字符个数
int s=0,j=0;
//进行匹配
while(s<=haystackLength-needleLength){
j=0;
while(haystackArray[s+j]==needleArray[j]){
j++;
if(j==needleLength){
return s;
}
}
if(s<haystackLength-needleLength){
s+=move[haystackArray[s+needleLength]];
}else{
return -1;
}
}
return -1;
}
}
欢迎来到这里!
我们正在构建一个小众社区,大家在这里相互信任,以平等 • 自由 • 奔放的价值观进行分享交流。最终,希望大家能够找到与自己志同道合的伙伴,共同成长。
注册 关于