全网最详细《红黑树》底层解析

一、红黑树的性质

每个节点要么是黑色，要么是红色。
根节点是黑色。
每个叶子节点（NIL）是黑色。
每个红色节点的两个子节点一定都是黑色。不能有两个红色节点相连。
任意一节点到每个叶子节点的路径都包含数量相同的黑结点。俗称：黑高！

从性质 5 又可以推出：性质 5.1：如果一个节点存在黑子节点，那么该结点肯定有两个子节点。

红黑树并不是一个完美平衡二叉查找树，从图上可以看到，根结点 P 的左子树显然比右子树高，但左子树和右子树的黑结点的层数是相等的，也即任意一个结点到到每个叶子结点的路径都包含数量相同的黑结点(性质 5)。所以我们叫红黑树这种平衡为黑色完美平衡。

二、红黑树的自平衡（左旋、右旋和变色）

1、变色

结点的颜色由红变黑或由黑变红。

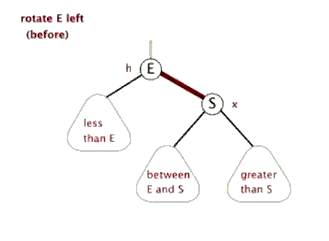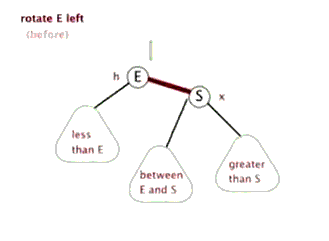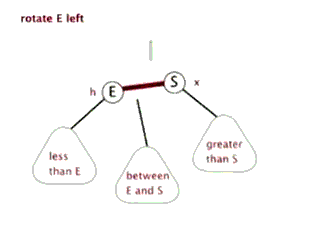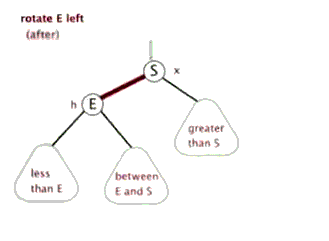
2、左旋

以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。

左旋图示：

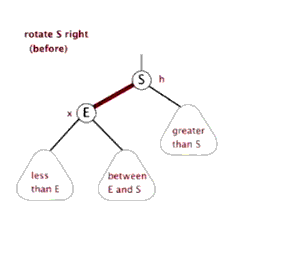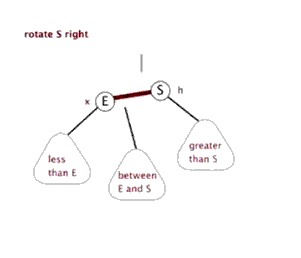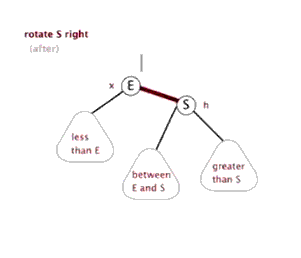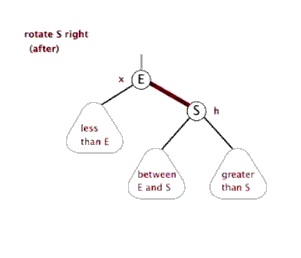
3、右旋

以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。

右旋图示：

三、红黑树的插入

插入操作包括两部分工作：

查找插入的位置。
插入后自平衡。

注意：插入节点，必须为红色，理由很简单，红色在父节点（如果存在）为黑色节点时，红黑树的黑色平衡没被破坏，不需要做自平衡操作。但如果插入结点是黑色，那么插入位置所在的子树黑色结点总是多 1，必须做自平衡。

红黑树插入节点情景分析

情景 1：红黑树为空树

最简单的一种情景，直接把插入结点作为根结点就行

**注意：**根据红黑树性质 2：根节点是黑色。还需要把插入结点设为黑色。

情景 2：插入结点的 Key 已存在

更新当前节点的值，为插入节点的值

情景 3：插入结点的父结点为黑结点

由于插入的结点是红色的，并不会影响红黑树的平衡，直接插入即可，无需做自平衡。

情景 4：插入节点的父节点为红色

根据红黑树的性质 2：根结点是黑色。如果插入节点的父结点为红结点，那么该父结点不可能为根结点，所以插入结点总是存在祖父结点。

这一点很关键，因为后续的旋转操作肯定需要祖父结点的参与。

插入情景 4.1：叔叔结点存在并且为红结点

依据红黑树性质 4 可知：红色节点不能相连 ==> 祖父结点肯定为黑结点；

因为不可以同时存在两个相连的红结点。那么此时该插入子树的红黑层数的情况是：黑红红。显然最简单的处理方式是把其改为：红黑红。

处理：

将 P 和 U 节点改为黑色
将 PP 改为红色
将 PP 设置为当前节点，进行后续处理

可以看到，我们把 PP 结点设为红色了，如果 PP 的父结点是黑色，那么无需再做任何处理；

但如果 PP 的父结点是红色，则违反红黑树性质了。所以需要将 PP 设置为当前节点，继续做插入操作自平衡处理，直到平衡为止。

插入情景 4.2：叔叔结点不存在或为黑结点，并且插入结点的父亲结点是祖父结点的左子结点

注意：单纯从插入前来看，叔叔节点非红即空（NIL 节点），否则的话破坏了红黑树性质 5，此路径会比其它路径多一个黑色节点。

插入情景 4.2.1：新插入节点，为其父节点的左子节点（LL 红色情况）

处理：

变颜色：将 P 设置为黑色，将 PP 设置为红色。
对 PP 节点进行右旋。

插入情景 4.2.2：新插入节点，为其父节点的右子节点（LR 红色情况）

处理：

对 P 进行左旋。
将 P 设置为当前节点，得到 LL 红色情况。
按照 LL 红色情况处理（1.变颜色 2.右旋 PP）。

插入情景 4.3：叔叔结点不存在或为黑结点，并且插入结点的父亲结点是祖父结点的右子结点

该情景对应情景 4.2，只是方向反转。

插入情景 4.3.1：新插入节点，为其父节点的右子节点（RR 红色情况）

处理：

变颜色：将 P 设置为黑色，将 PP 设置为红色。
对 PP 节点进行左旋。

插入情景 4.3.2：新插入节点，为其父节点的左子节点（RL 红色情况）

处理：

对 P 进行右旋。
将 P 设置为当前节点，得到 RR 红色情况。
按照 RR 红色情况处理（1.变颜色 2.左旋 PP）。

总结：

    /**
     * 插入后修复红黑树平衡的方法
     * |---情景1：红黑树为空树
     *              处理：直接把插入结点作为根结点。
     * |---情景2：插入节点的key已经存在
     *              处理：更新当前节点的值，为插入节点的值。
     * |---情景3：插入节点的父节点为黑色
     *              处理：直接插入即可。
     * |---情景4：插入节点的父节点为红色
     * |---情景4.1：叔叔节点存在，并且为红色（父-叔 双红）
     *                处理：父亲和叔叔节点改为黑色，爷爷节点改为红色，将爷爷节点设为当前节点继续平衡处理。
     * |---情景4.2：叔叔节点不存在，或者为黑色，父节点为爷爷节点的左子树
     * |---情景4.2.1：插入节点为其父节点的左子节点（LL情况）
     *                  处理：父亲节点改为黑色，爷爷节点改为红色，对爷爷节点进行右旋
     * |---情景4.2.2：插入节点为其父节点的右子节点（LR情况）
     *                  处理：对父亲节点进行左旋，得到LL情况，按照LL情况继续处理。
     * |---情景4.3：叔叔节点不存在，或者为黑色，父节点为爷爷节点的右子树
     * |---情景4.3.1：插入节点为其父节点的右子节点（RR情况）
     *                  处理：父亲节点改为黑色，爷爷节点改为红色，对爷爷节点进行左旋
     * |---情景4.3.2：插入节点为其父节点的左子节点（RL情况）
     *                  处理：对父亲节点进行右旋，得到RR情况，按照RR情况继续处理。
     */

四、二叉树的删除

删除操作包括两部分工作：

替换删除节点到合适位置并自平衡
删除节点

红黑树删除节点情景分析

情景 1：节点的左子树、右子树都不为 null

针对这种情况，通常为了简化操作，都会采用左子树的最大子节点或者右子树的最小子节点的值来替换当前节点的值，然后删除左子树的最大子节点或右子树的最小子节点，替换后需要删除的节点的可能情况为其他三种。

情景 2：节点的左子树为 null、右子树不为 null 或者右子树为 null，左子树不为 null

以下情景以左 null 右非 null 为例：

情景 2.1：需要删除的节点为红色节点

根据红黑树的性质，其右子节点不可能为红色（违反性质 4），不可能出现右子节点是黑色节点的情况（违反性质五）；所以右子节点只可能是 NIL，直接删除该节点即可。

情景 2.2：需要删除的节点为黑色节点

根据红黑树的性质，其右子节点要么就是 NIL,要么是红色节点，且该红色节点的两个子节点为 NIL。

如果右子节点为 NIL 则符合左右子树都为 null 的情景，详见情景 3 解析；
如果右子节点为红色，则把右子节点变成黑色并顶替该节点即可。

情景 3：两个子树均为 null

以下情景以该节点为父节点的左子节点为例：

情景 3.1：需要删除的节点为红色节点

直接删除该节点即可。

情景 3.2：需要删除的节点为黑色节点

因为该节点为黑色节点，删除该节点会导致该路径上的黑色节点数量 -1，并且因为没有子节点，根本无法通过子树内部修正路径；所以得考虑从该节点的兄弟节点处入手，让他匀一个黑色节点过来，因为该节点为黑色节点，所以其兄弟节点必然存在（性质 5.1）且可能是红色节点，也可能是黑色节点。

情景 3.2.1：该节点的兄弟节点为红色

他们的父节点一定是黑色节点。

处理：

将兄弟节点变为黑色，父亲节点变为红色
如果该节点为父节点的左子节点，则对父节点进行左旋处理，反之则进行右旋处理。

此时情景转化为 3.2.2。

-->

情景 3.2.2：该节点的兄弟节点为黑色

他们的父节点则颜色不定。

情景 3.2.2.1：该节点的远侄子节点为红色且该节点为父节点的左子节点

没有上色的节点表示黑色红色均可，注意如果 SL 为黑色，则 SL 必为 NULL 节点。

处理：

将 P 和 S 的颜色对调。
对 P 节点进行左旋处理。
把 SR 节点变成黑色，并删除 D 即可。

-->

情景 3.2.2.2：该节点的远侄子节点为红色且该节点为父节点的右子节点

处理：

将 P 和 S 的颜色对调。
对 P 节点进行右旋处理。
把 SL 节点变成黑色，并删除 D 即可

-->

情景 3.2.2.3：远侄子节点为黑色，近侄子节点为红色，该节点为父亲节点的左孩子

处理：

SL 节点颜色设为 P 节点颜色。
将 P 节点颜色设为黑色。
将 S 节点右旋。
将 P 节点左旋。

情景 3.2.2.4：远侄子节点为黑色，近侄子节点为红色，该节点为父亲节点的右孩子

处理：

SR 节点颜色设为 P 节点颜色。
将 P 节点颜色设为黑色。
将 S 节点左旋。
将 P 节点右旋。

情景 3.2.3：父亲节 p 为红色，兄弟节点和兄弟节点的两个孩子（只能是 NULL 节点）都为黑色

处理：

将父亲节点 P 改成黑色，将兄弟节点 S 改成红色。
然后删除 D 即可。

-->

情景 3.2.4：父亲节点 p，兄弟节点 s 和兄弟节点的两个孩子（只能为 NULL 节点）都为黑色

处理：

将兄弟节点 S 的颜色改成红色。
然后删除 D。
以 P 为起始节点继续进行自平衡操作。

-->

总结：

/**
     * 删除红黑树自平衡方法
     *
     * |---情景1：左右子树均不为空
     *              处理：寻找后继节点进行替换操作，更新待平衡节点为替换后的节点。
     * |---情景2. 左右子树有一个为空
     * |---情景2.1：需要删除的节点为红色节点
     *                处理：直接删除。
     * |---情景2.2：需要删除的节点为黑色节点
     *                处理：如果一个子节点为红色，则把子节点变成黑色并替换该节点，删除替换后的节点。
     * |---情景3：两个子树均为null
     * |---情景3.1：需要删除的节点为红色节点
     *                处理：直接删除。
     * |---情景3.2：需要删除的节点为黑色节点
     * |---情景3.2.1：该节点的兄弟节点为红色
     *                  处理：将兄弟节点变为黑色，父亲节点变为红色，
     *                        若该节点为父节点的左子节点，则对父节点进行左旋处理，反之则进行右旋处理
     *                        此时情景转化为3.2.2。
     * |---情景3.2.2：该节点的兄弟节点为黑色
     * |---情景3.2.2.1：该节点的远侄子节点为红色且该节点为父节点的左子节点
     *                    处理：将父节点和兄弟节点的颜色对调。
     *                          对父节点进行左旋处理。
     *                          把远侄子节点变成黑色，并删除目标节点即可。
     * |---情景3.2.2.2：该节点的远侄子节点为红色且该节点为父节点的右子节点
     *                    处理：将父节点和兄弟节点的颜色对调。
     *                          对父节点进行右旋处理。
     *                          把远侄子节点变成黑色，并删除目标节点即可。
     * |---情景3.2.2.3：远侄子节点为黑色，近侄子节点为红色，该节点为父亲节点的左孩子
     *                    处理：将近侄子节点颜色设为父节点颜色。
     *                          将父节点颜色设为黑色。
     *                          将兄弟节点右旋。
     *                          将父节点节点左旋。
     * |---情景3.2.2.4：远侄子节点为黑色，近侄子节点为红色，该节点为父亲节点的右孩子
     *                    处理：将近侄子节点颜色设为父节点颜色。
     *                          将父节点颜色设为黑色。
     *                          将兄弟节点左旋。
     *                          将父节点节点右旋。
     * |---情景3.2.3：父亲节为红色，兄弟节点和兄弟节点的两个孩子（只能是NULL节点）都为黑色
     *                  处理：将父节点改成黑色，将兄弟节点改成红色。
     *                        然后删除目标节点即可。
     * |---情景3.2.4：父亲节点，兄弟节点和兄弟节点的两个孩子（只能为NULL节点）都为黑色
     *                  处理：将兄弟节点改成红色。
     *                        删除目标节点。
     *                        以父节点为目标节点继续进行自平衡操作
     *
     */

五、手撕代码

码云链接：https://gitee.com/wlgzs-sjl/HongHeiShu

欢迎 star 支持！

参考博客：

https://my.oschina.net/u/3272058/blog/1914452

红黑树之删除节点 - 青儿哥哥 - 博客园